什么是排序
输入
输入一段序列
输出
输出该序列的有序序列
算法的稳定性
对于A与B,其关键字相同,若排序后,A与B的相对位置仍不变,则称该算法是稳定的。
分类:根据元素是否完全存在于内存中
- 内部排序:排序期间元素全部在内存中。
- 外部排序:排序期间元素无法全部同时存在于内存中。
插入排序
直接插入排序
将数据分为“有序部分、待确定元素、无需部分”,慢慢扩大有序部分,缩小无需部分,直至全部有序。
算法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| void InsertSort(ElemType a[],int n){
int i = 2,j = 0;
while(;i<=n;i++){
if(a[i] < a[i-1]){
a[0] = a[i];
for(j=i-1;a[0]<a[j];j--){
a[j+1] = a[j];
}
a[j+1] = a[0];
}
}
}
|
分析
- 空间复杂度O(1)
- 比较次数和移动次数取决于排序表的初始状态。一种理解时间复杂度的方式最好O(n),即执行n次if条件判断语句,不执行元素移动;最坏O(n^2),即i=2时,移动一次元素、i=3时,移动两次元素······,即为1+2+···+(n-1)=n*(n-1)/2,赋值语句不计入比较。
- 时间复杂度O(n^2)
- 是稳定的算法
- 适用于顺序存储和链式存储的线性表,采用链式存储是无需移动元素
- 适用于基本有序的排序表或数据量不大的排序表
折半插入排序
直接插入排序进行了:找到位置+移位操作 - - - 一边比较一边移动元素
折半插入排序:找到位置+移位操作 - - - 直接找到待插位置+将整体部分一个个移动
算法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| void InsertSort(ElemType a[],int n){
int i , j , high , mid;
for(i = 2;i<=n;i++){
a[0] = a[i];
low = 1 ;
high = i-1;
while(low <= high){
mid = (low+high)/2;
if(a[mid]>a[0]){
high = mid-1;
}else{
low =mid+1;
}
}
for(j = i-1;j>=high+1;--j){
a[j+1] = a[j];
}
a[high+1] = a[0];
}
}
|
分析
- 折半插入仅减小了比较的次数
- 仅适用于顺序表
- 稳定的
两种排序方法的比较


希尔排序
mini版直接插入排序,因为直接插入排序当序列为排列好时,时间复杂度最小。顾希尔排序为了让其接近于有序。
过程:取一个小于n的增量d1,把表分为d1组(即这次有d1个下凹槽),对这d1组分别执行直接插入排序;接着取d2<d1,直至dn = 1
算法
分析
- 不稳定
- 空间复杂度O(1)
- O(n^1.3),当n在某个范围内时(很难计算出1.3);O(n^2),最坏。
- 适用于顺序表
交换排序
根据两个关键字的比较结果来交换这两个元素的位置
冒泡排序
算法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| void BubbleSort(ElemType a[],int n){
for(int i = 0 ; i< n-1;i++){
bool flag = false;
for(int j = n-1;j>i;j--){
if(a[j]<a[j-1]){
int temp = a[j];
a[j] = a[j-1];
a[j-1] = temp;
flag = true;
}
}
if(flag == false){
return;
}
}
}
|
分析

- 空间复杂度O(1)
- 只有小于时交换,因此这位稳定的算法
- 适用于顺序表与链表
- 不同于直接插入排序,冒泡排序产生的有序子序列是全局有序的。

快速排序
算法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
void QuickSort(ElemType a[],int low,int high){
if(low < high){
int pivotpos = Partition(a,low,high)
QuickSort(a,low,pivotpos-1);
QuickSort(a,pivotpos+1,high);
}
}
int Partition(ElemType a[],int low ,int high){
ElemType pivot = a[low]; 将当前表中的第一个元素设为枢轴,划分表
while(low < high){
while(low < high && a[high]>=pivot) --high;
a[low] = a[high];
while(low < high && a[low]<=pivot) ++low;
a[high] = a[low];
}
a[low] = pivot;
return low;
}
|
分析


- 仅适用于顺序表
- 不稳定
- 为什么说元素二等分时最快,有序时最慢:这些都在在pivot选择每份元素第一个值的条件下运作的。
选择排序
简单选择排序
算法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| void SelectSort(ElemType a[],int n){
for(int i = 0 ; i < n-1;i++){
int min = i;
for(int j =i+1;j<n;j++){
if(a[j] < a[min]){
min = j;
}
}
if(min != i){
int temp = a[min];
a[min] = a[i];
a[i] = temp;
}
}
}
|
分析
- 简单选择排序:设第一个元素为最小值,向后查找,若遇到比它小的元素,更新min值;最后交换这两个数。
- 空间复杂度O(1)
- 时间复杂度:比较次数:和初始排序的序列无关为
n*(n-1)/2;操作次数最大3*(n-1),最小0。时间复杂度始终是O(n^2)
- 不稳定,可由(2,2‘,1)验证
- 适用于顺序表与链表
堆排序
- 大根堆:一棵完全二叉树,任何一个非叶节点大于等于左右孩子节点
- 小根堆:一棵完全二叉树,任何一个非叶节点小于等于左右孩子节点
- 思路:1->将一个无序序列构造为堆;2->当堆顶元素不在时,如何调整堆以便下一次删除堆顶元素
算法
- 性质:对于有n个节点的完全二叉树,它层次遍历的最后一个节点,就是
n/2向下取整的孩子
- 建立堆的思想:遍历
n/2向下取整#到#1,设其为k,若k小于左右孩子中的较大者,则让他们交换。这个过程可能会破坏下一级的堆,需重新构造。
- 建立大根堆
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| void BuildMaxHeap(ElemType a[],int len){
for(int i = len/2;i>0;i--){
HeadAdjust(a,i,len);
}
}
void HeadAdjust(ElemType a[],int k,int len){
a[0] = a[k];
for(int i = 2*k;i<=len;i*=2){
if(i < len && a[i]<a[i+1]){
i++;
}
if(a[0] > a[i]){
break;
}
else{
a[k] = a[i];
k = i;
}
}
a[k] = a[0];
}
|
- 堆排序算法
1
2
3
4
5
6
7
8
| void HeapSort(ElemType a[],int len){
BuildMaxHeap(a,len);
for(int i = len;i>1;i--){
Swap(a[i],a[1]);
HeadAdjust(a,1,i-1);
}
}
|
分析

- 根据算法可得,关键字的总比较次数不超过
4*n。即总调整次数*每次调整所需要比较4次。
- 空间复杂度:O(1)
- 不稳定
- 适用于顺序表
归并排序
算法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
|
ElemType *b = (ElemType*)malloc(sizeof(ElemType) * (n+1));
void Merge(int a[],int low,int mid, int high){
int k = 0;
for(int k = low ;k <= high ;k++){
b[k] = a[k];
}
int i = 0 , j = 0;
for(i = low , j = mid+1 , k = i;I<=mid && j <=high;k++){
if(b[i] <= b[j]){
a[k] = b[i++];
}else{
a[k] = b[j++];
}
}
while(i <= mid){
a[k++] = b[i++];
}
while(j <= high){
a[k++] = b[j++];
}
}
void MergeSort(ElemType a[],int low,int high){
if(low < high){
int mid = (low+high)/2;
MergeSort(a,low,mid);
MergeSort(a,mid+1,high);
Merge(a,low,mid,high);
}
}
|
分析
- 归并:将两个或者两个以上的有序表合并成为新的有序表
- 二路归并排序:将有n个元素的表视为n个长度为1的表,两两合一,成为n/2(向上取整)个长度为1或者2的
部分有序表;继续两两归并,直至成为一个长度为n的有序表。
- 空间复杂度:O(n),对辅助数组的重复利用
- 时间复杂度:可参考建堆时间复杂度,为
O(n)*⌈log2n⌉ = O(n*log2n)
- 稳定
- 使用于顺序表与链表
- 对于k路归并排序,所需要的趟数为
⌈logkn⌉
- **注意:**归并本身并不涉及排序,只是合并已排序的有序段
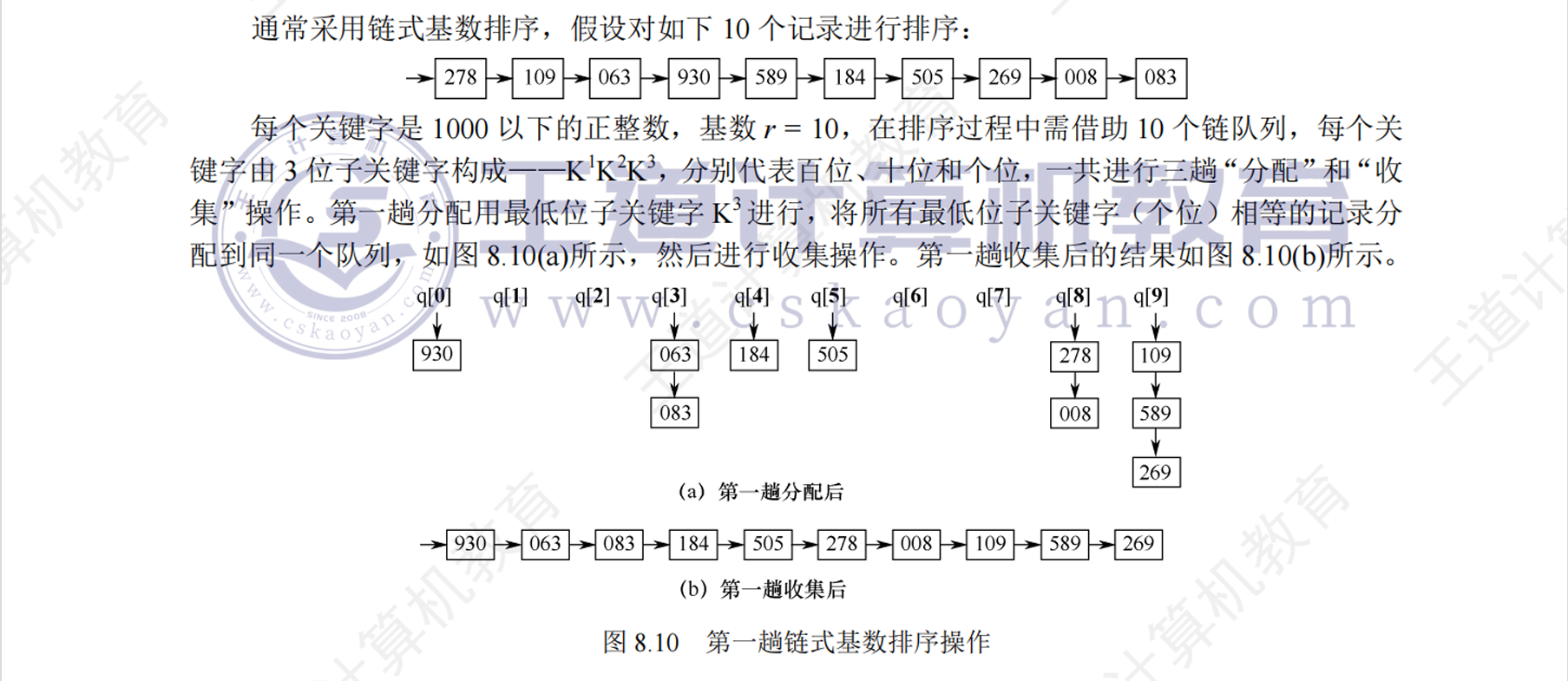
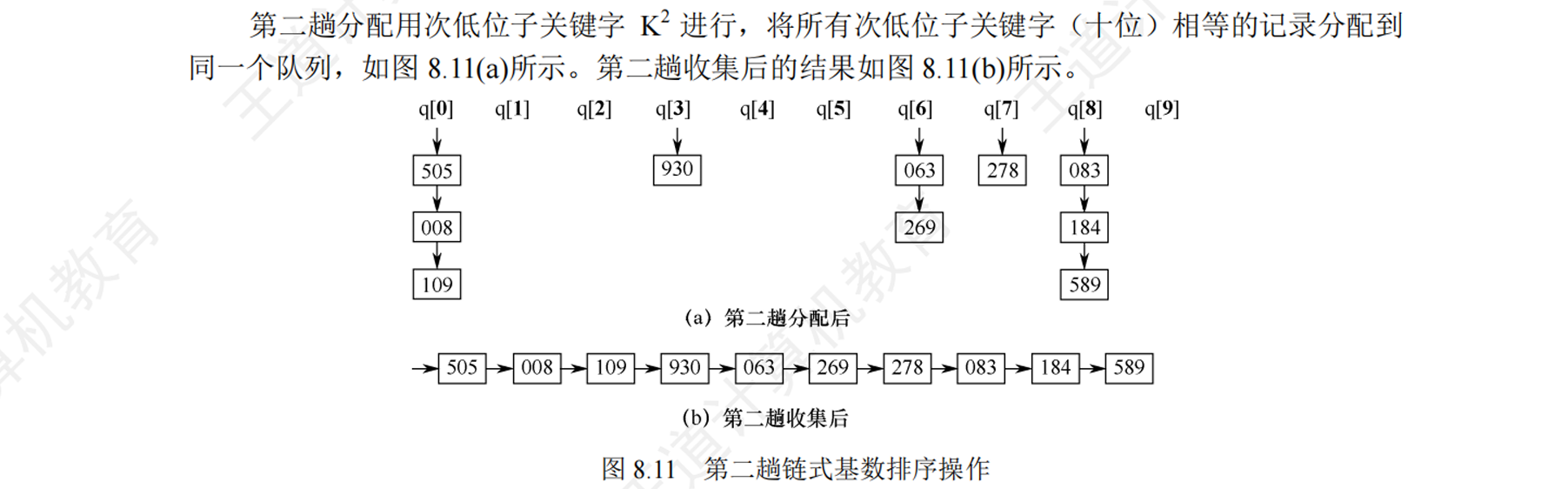
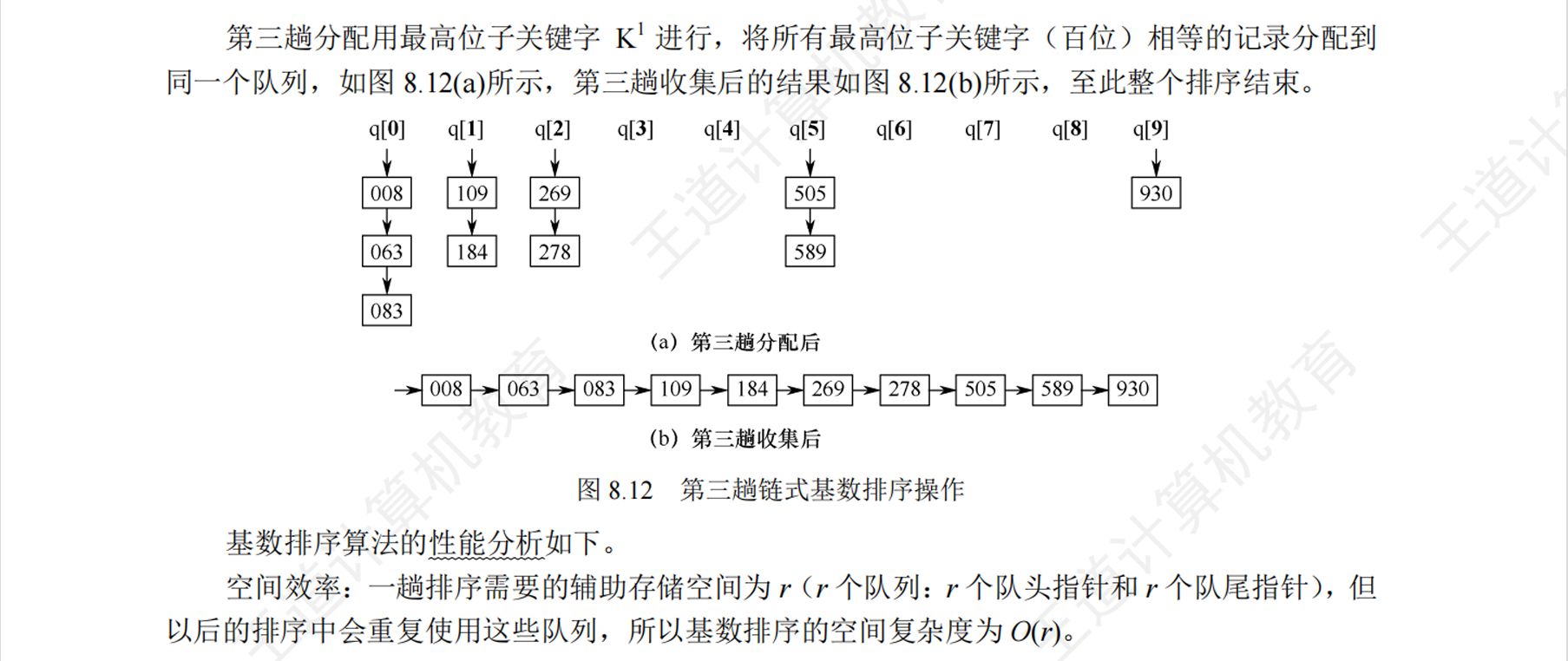
基数排序
算法
略
分析
- 不基于比较与移动
- 基数(Radix)(r)指的是数字或字符的进制基数,数字为十进制,基数为10

计数排序
算法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| void CountSort(ElemType a[],ElemType b[],int n, int k){
int i = 0,c[k];
for(i = 0;i < k;i++){
c[i] = 0;
}
for(i = 0 ; i < n;i++){
c[a[i]]++;
}
for(i = 1 ;i < k;i++){
c[i] = c[i] + c[i-1];
}
for(i = n-1;i>=0;i--){
b[c[a[i]] - 1] = a[i];
c[a[i]] = c[a[i]] - 1;
}
}
|
分析

- 注意:

- k = O(n) 表示数据范围 k 和元素数量 n 同数量级(即 k 不超过 n 的常数倍)。
- k > O(nlog₂n)可以表示:k 的增长速度快于 nlog₂n
外部排序
外部排序的方法
- 怎么排序:采用归并排序->1. 将外存中的文件分为l份,依次读入内存,依次使用内排排序,再写入外存 2. 对这些归并段归并
- 详细介绍:

- 输入、输出缓冲区:

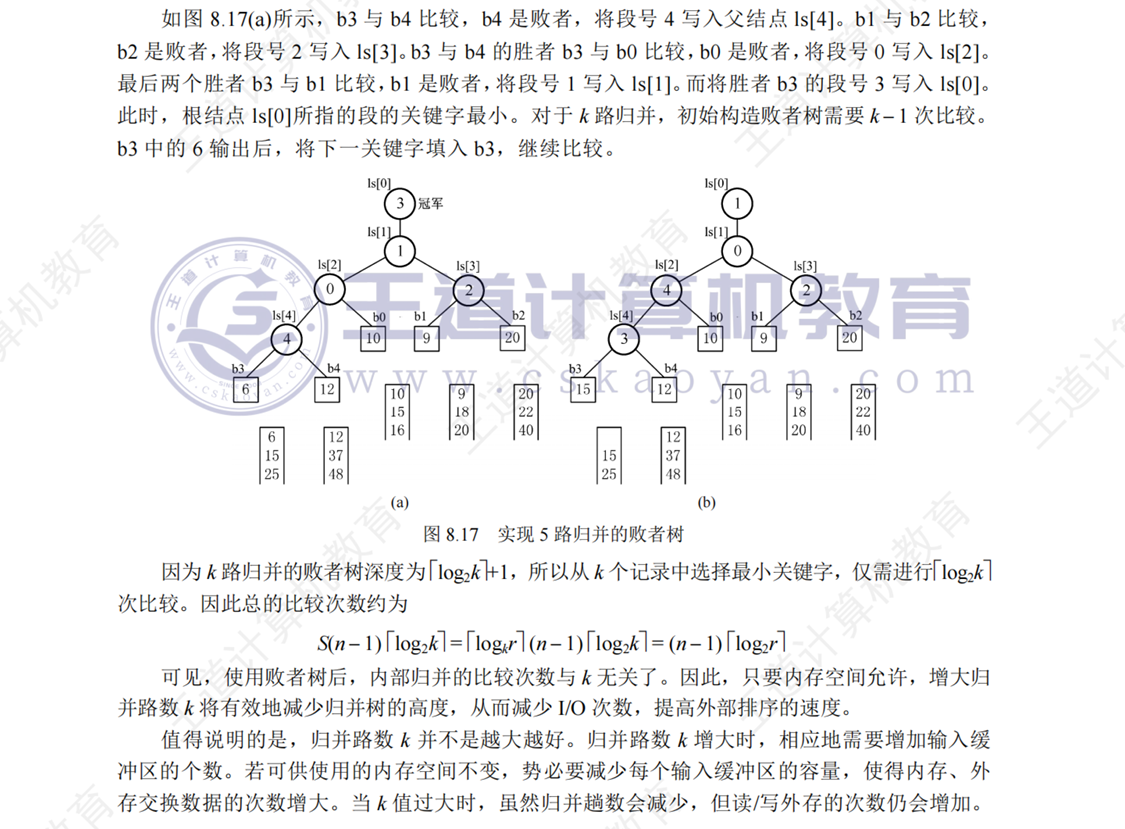
多路平衡归并与败者树
分析
置换、选择排序
最佳归并树
练习
1

这道题可以使用冒泡排序的思想,但时间复杂度会达到O(n^2)。接下来使用一种基于快排思想的方法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| void Sort(int a[],int n){
int i = 0 , j = n-1;
while(i < j){
while(i < j && [i]%2 != 0){i++};
while(i < j && [j]%2 == 0){j--};
if(i < j){
int temp = a[i];
a[i] = a[j];
a[j] = temp;
}
i++;
j--;
}
}
|
2

很容易想到先排序后定位,但这样时间O(n*logn)是最小的。
接下来介绍平均时间复杂度为O(n)的算法:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
int kth_elem(int a[],int low,int high,int k){
int pivot = a[low];
int low_temp = low;
int high_temp = high;
while(low < high){
while(low < high && a[high]>pivot){high--;}
a[low] = a[high];
while(low < high && a[low] < pivot){low++;}
a[high] = a[low];
}
a[low] = pivot;
int rank = low -low_temp+1;
if(rank == k){
return a[low];
}else if(rank > k){
kth_elem(a,low_temp,low-1,k);
}else{
kth_elem(a,low+1,high_temp,k-rank);
}
}
|