数据结构-图
图的基本概念
图G由顶点V和边E组成,记为G=(V,E),V一定非空,E可以空。
V={v1,v2,……,vn},|V|表示顶点个数
E={(u,v)|u∈V,v∈V},|E|表示边的条数
有向图
<v,w>称为从v到w的弧,也称v邻接到w。v为弧尾,w为弧头。无向图
(v,w)或者(w,v)说,w与v互为邻接点简单图与多重图
简单图:1-不存在重复边(两个顶点的边数不多于一条);2-不存在到自身的边
多重图:反之完全图
若图的顶点数为n,如果|E|=n*(n-1)/2,称为无向完全图;如果|E|=n*(n-1),称为有向完全图。子图
设有两个图G=(V,E),G’=(V’,E’),若V’∈V,E’∈E,则称G’是G的子图。生成子图
若满足V(G’) = V(G),则称G’为G的生成子图连通、连通图、连通分量(无向图范畴)
连通:两点之间存在路径
连通图:任意两点之间都是连通的
连通分量:无向图中的极大连通子图
若一个图有n个顶点,若边数小于n-1,则为非连通图;若它是非连通图,则边数最多为
(n-1)(n-2)/2
- 强连通、强连通图、强连通分量(有向图范畴)
强连通:两点之间有双向路径
强连通图:任意两点之间都是强连通的
强连通分量:~
若一个有向图有n个顶点,若其为强连通图,最少需要n条边。
- 生成树
连通图的生成树:包含全部顶点的极小连通子图(顶点数若为n,则其边数为n-1)
生成森林:在非连通图中,连通分量的生成树构成了非连通图的生成森林
极大||极小 - 连通子图:前者:尽可能包含多的点与边;后者:尽可能少的包含边。
顶点的度、入度、出度
无向图中:度(TD):依附于顶点的边的条数。度数和=边数*2。
有向图中:入度(ID):以顶点为终点的有向边的数目
出度(OD):以顶点为起点的有向边的数目
度:结点的入度加出度
入度之和等于出度之和等于边数
边的权、网
边上的权值。带权的图成为带权图,也成为网弧
有向图的边稠密图、稀疏图
只是模糊的相对的概念。一般当|E|<|V|log|V|时,将其视为稀疏图路径、路径长度、回路
路径:指的是顶点序列(eg:v1,v2,v3)
路径长度:路径上边的数目
回路(环):第一个顶点和最后一个顶点相同的路径。n个顶点的图中,若路径大于n-1,则存在回路。简单路径、简单回路
简单路径:顶点不重复出现
简单回路:除第一个顶点、最后一个顶点,其他顶点不重复出现的回路。距离
两个顶点间的最短路径,若不存在则为∞有向树
有向图满足一个顶点入度为0,其余顶点入度均为1。
图的存储及其基本操作
邻接矩阵法(adjacency matrix)
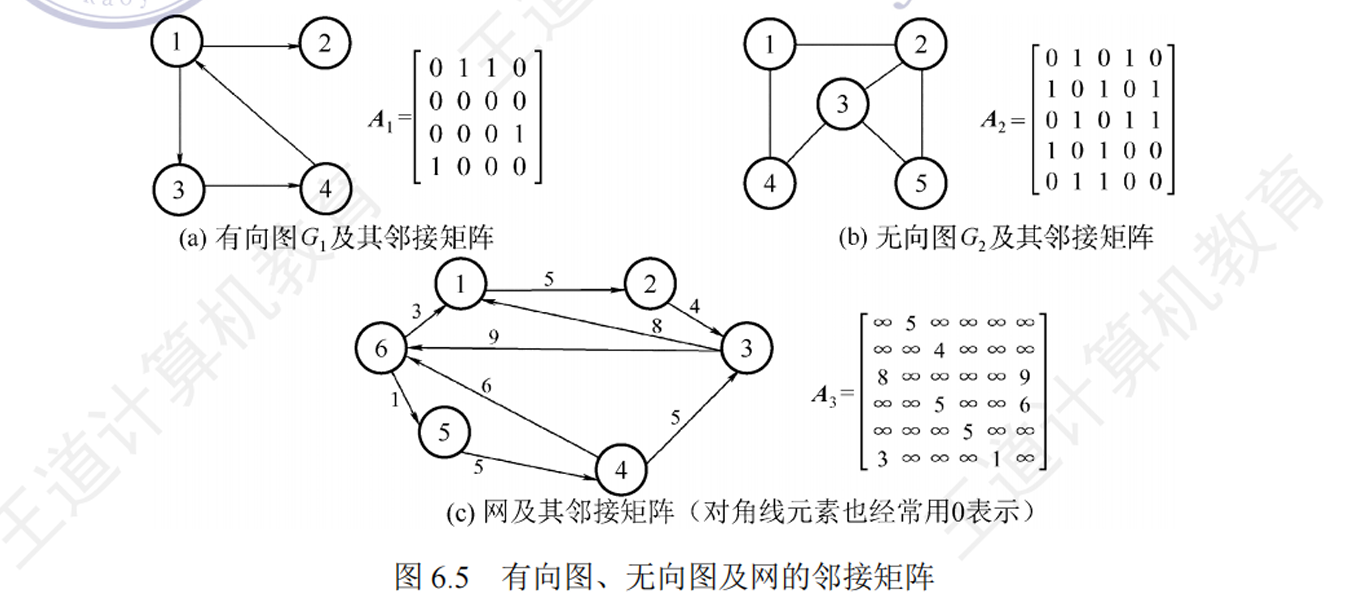
1 |
|
- 空间复杂度为O(n^2),其中n为顶点的个数
- 当仅表示边是否存在时,可以用0\1的枚举类型定义边表
- 基于邻接矩阵度的计算
- 无向图:结点i的度,为第i行非0\∞元素的个数
- 有向图:结点i的出度,为i行非0\∞元素个数;结点i的入度,为第i列非0\∞元素的个数
- 用邻接矩阵很容易确定两个结点间是否有边;但确定总边数花费较大。
- 稠密图适合采用邻接矩阵
- 若一个图的邻接矩阵为A,则
A^n[i][j]代表从结点i到结点j的路径长度为n的个数(参考离散数学)
邻接表法(adjacency list)
为减少邻接矩阵的浪费而生,采用顺序存储结合链式存储
1 |
|
- 为什么要区分
- 顶点和边的性质不同:
顶点是图的基本单元,通常包含额外的信息(如名称、权重等)。
边表示顶点之间的关系,通常只关注连接的目标顶点和边的权重(如果有)。
- 存储结构不同:
顶点表是一个数组或链表,存储所有顶点的信息。
边表是一个链表,存储与某个顶点相连的所有边。
- G为无向图,则所需的存储空间为:O(|V|+2|E|);G为由向图,则所需的存储空间为:O(|V|+|E|)
- 稀疏图可采用邻接表法,节省空间
- 给顶点,找到临边容易。
- 无向图求顶点的度:遍历该结点对应的边表。有向图由出度:同上。有向图求入度,遍历所有顶点的边表。
- 一个图的邻接表不唯一
- 若有向图使用邻接表法表示,有n个顶点,e条边。若删除与顶点v相关的所有边:
需要删除顶点v的入边与出边
以下是删除顶点 v所有入边的伪代码:
1 | def delete_in_edges(v): |
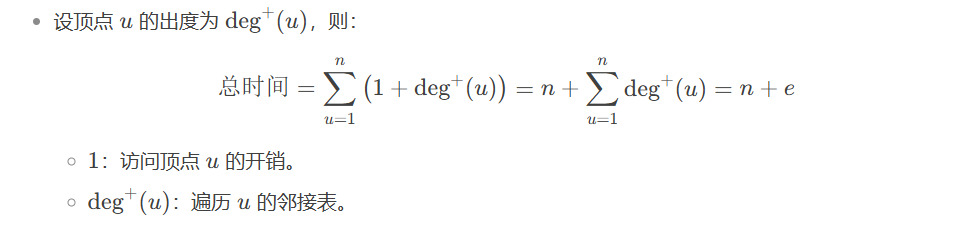
以下删除出边
- 对于n个顶点,e条边的无向图:建立邻接表,需要n+2*e次操作,时间复杂度为O(n+e)
十字链表
是有向图的链式存储结构。
每个弧用一个结点表示,每个顶点也用一个结点表示
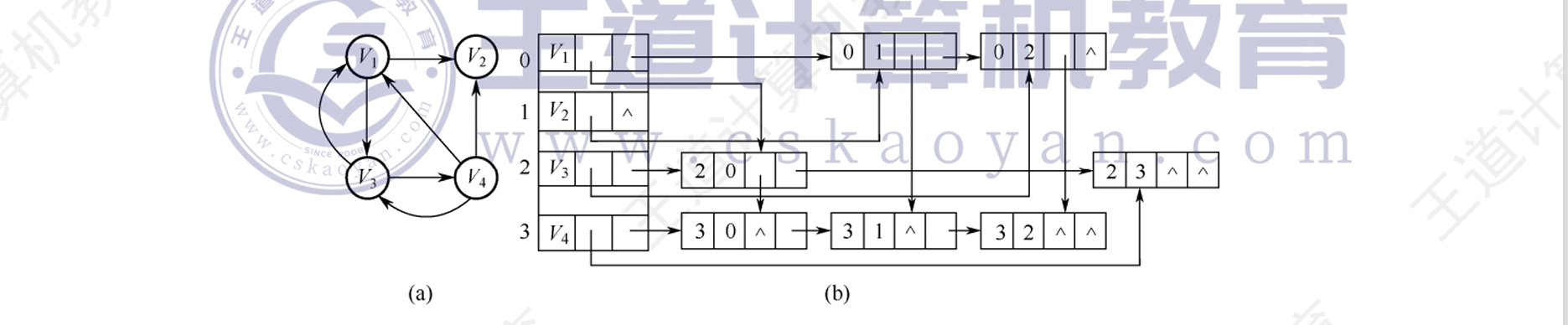
- 弧结点
- TailVertex:弧尾编号
- HeadVertex:弧头编号
- hlink:弧头相同的下一个结点
- tlink:弧尾相同的下一个结点
- info:弧的相关信息
- 顶点结点
- data:顶点相关信息
- firstin:第一个弧头朝向该顶点的弧
- fitstout:第一个弧尾朝向该顶点的弧
- 十字链表容易确定出度与入度
- 图的十字链表不唯一,然而一个十字链表可以确定一个唯一的图
邻接多重表
无向图的链式存储结构
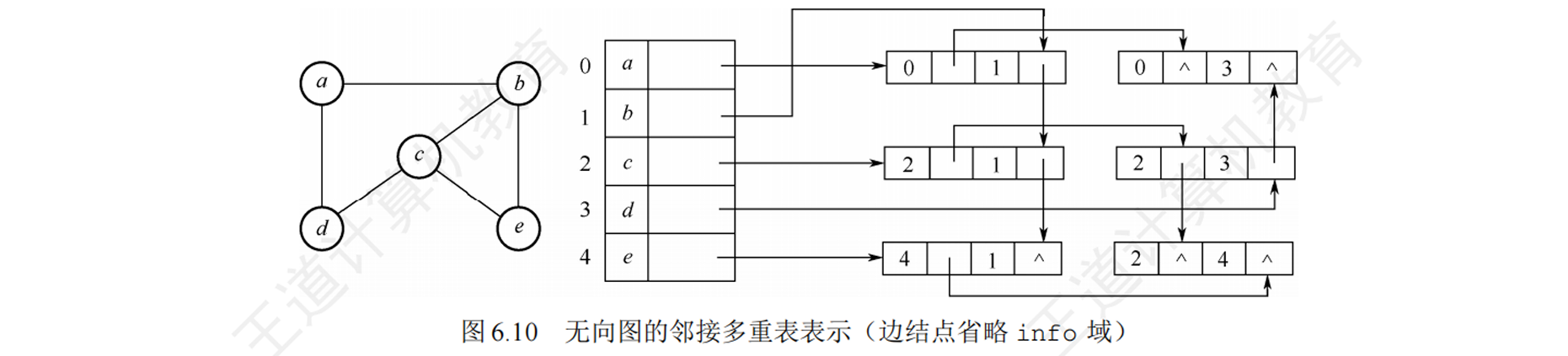
- 边结点
- ivex:指示该边依附的两个顶点的编号之一
- ilink:下一条依附于顶点ivex的边
- jvex:指示该边依附的两个顶点的编号之一
- jlink:下一条依附于jvex的边
- info:信息
- 顶点结点
- data
- firstedge:第一条依附于该顶点的边
图的遍历
对图中所有顶点访问、且只访问一次
广度优先搜索BFS
- 伪代码
1 | bool visited[max]; |
- 用邻接表实现BFS
1 | void BFS(ALGraph G,int i){ |
- 使用邻接矩阵实现BFS
1 | void BFS(MGraph G,int i){ |
BFS性能分析
- 空间复杂度:涉及到辅助队列,为O(|V|)
- 时间复杂度:

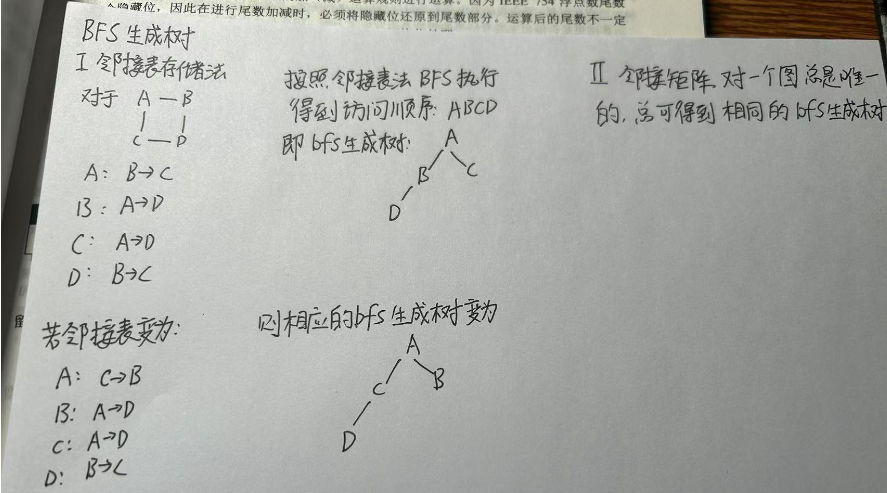
BFS单源最短路径
1 | void BFS_Mini_Distance(Graph G,int u){ |
深度优先搜索DFS
- 代码
1 | bool visited[max]; |
- DFS的实现(使用邻接表)
1 | void DFS(ALGraph G,int i){ |
- DFS的实现(使用邻接矩阵)
1 | void DFS(MGraph G,int i){ |






