数据结构-查找

顺序查找和折半查找

顺序查找

1. 可分为一般线性表的顺序查找和按关键字的有序线性表的查找
2. 适用于顺序表与链表。遍历方式为下标与next指针。

一般线性表的顺序查找

typedef struct {
    ElemType *data;
    int length;
}SeqList;

int Search_Seq(SeqList L,ElemType key){
    L.data[0] = key;        //sentry
    while(int i = L.length;L.data[i] != key;--i);
    return i;
}

/*
定义length为5，数组下标1-5为存储data单元，0作为哨兵（本题中）
*/

上面代码引入了“哨兵”，用于避免不必要的判断语句。就其而言，不用些越界判断条件i>=0了

那么能不能在链式存储结构中使用哨兵呢？看看下面这个代码

#include <stdio.h>
#include <stdlib.h>

// 定义元素类型和链表节点
typedef int ElemType; // 假设元素类型为 int
typedef struct LNode {
    ElemType data;          // 数据域
    struct LNode *next;     // 指针域
} LNode, *LinkList;

// 顺序查找函数（带哨兵）
LNode* seq_search_with_sentinel(LinkList L, ElemType key) {
    if (L->next == NULL) {
        return NULL; // 链表为空，直接返回 NULL
    }

    // 创建哨兵节点，并将其值设置为 key
    LNode sentinel;
    sentinel.data = key;
    sentinel.next = NULL;

    // 将哨兵节点添加到链表的末尾
    LNode *p = L->next; // 指向首元节点
    while (p->next != NULL) {
        p = p->next;
    }
    p->next = &sentinel; // 将哨兵节点链接到链表末尾

    // 查找过程
    LNode *p_find = L->next; // 从头节点的下一个节点开始查找
    while (p_find->data != key) {
        p_find = p_find->next;
    }

    // 恢复链表结构，移除哨兵节点
    p->next = NULL;

    // 判断是否找到目标节点
    if (p_find != &sentinel) {
        return p_find; // 找到目标节点
    } else {
        return NULL; // 未找到目标节点
    }
}

// 创建链表（头插法）
void create_list(LinkList L, ElemType arr[], int n) {
    L->next = NULL; // 初始化头节点
    for (int i = 0; i < n; i++) {
        LNode *new_node = (LNode *)malloc(sizeof(LNode));
        new_node->data = arr[i];
        new_node->next = L->next;
        L->next = new_node;
    }
}

// 打印链表
void print_list(LinkList L) {
    LNode *p = L->next;
    while (p != NULL) {
        printf("%d -> ", p->data);
        p = p->next;
    }
    printf("NULL\n");
}

int main() {
    // 初始化链表
    LinkList L = (LinkList)malloc(sizeof(LNode)); // 创建头节点
    ElemType arr[] = {3, 1, 4, 1, 5, 9, 2, 6};
    int n = sizeof(arr) / sizeof(arr[0]);
    create_list(L, arr, n);

    // 打印链表
    printf("链表内容: ");
    print_list(L);

    // 查找测试
    ElemType key = 5;
    LNode *result = seq_search_with_sentinel(L, key);
    if (result != NULL) {
        printf("找到元素: %d\n", result->data);
    } else {
        printf("未找到元素: %d\n", key);
    }

    // 释放链表内存
    LNode *p = L->next;
    while (p != NULL) {
        LNode *temp = p;
        p = p->next;
        free(temp);
    }
    free(L);

    return 0;
}

结合“将哨兵节点添加到链表的末尾”，说明需要遍历两次链表，虽然时间复杂度仍是O(n)，但意义并不大。

总结：

1. ASL_S=(n+1)/2 ASL_F=n+1:(比较次数)
2. 缺点，n较大时效率低

有序线性表的顺序查找

1. 不成功时的ASL
   

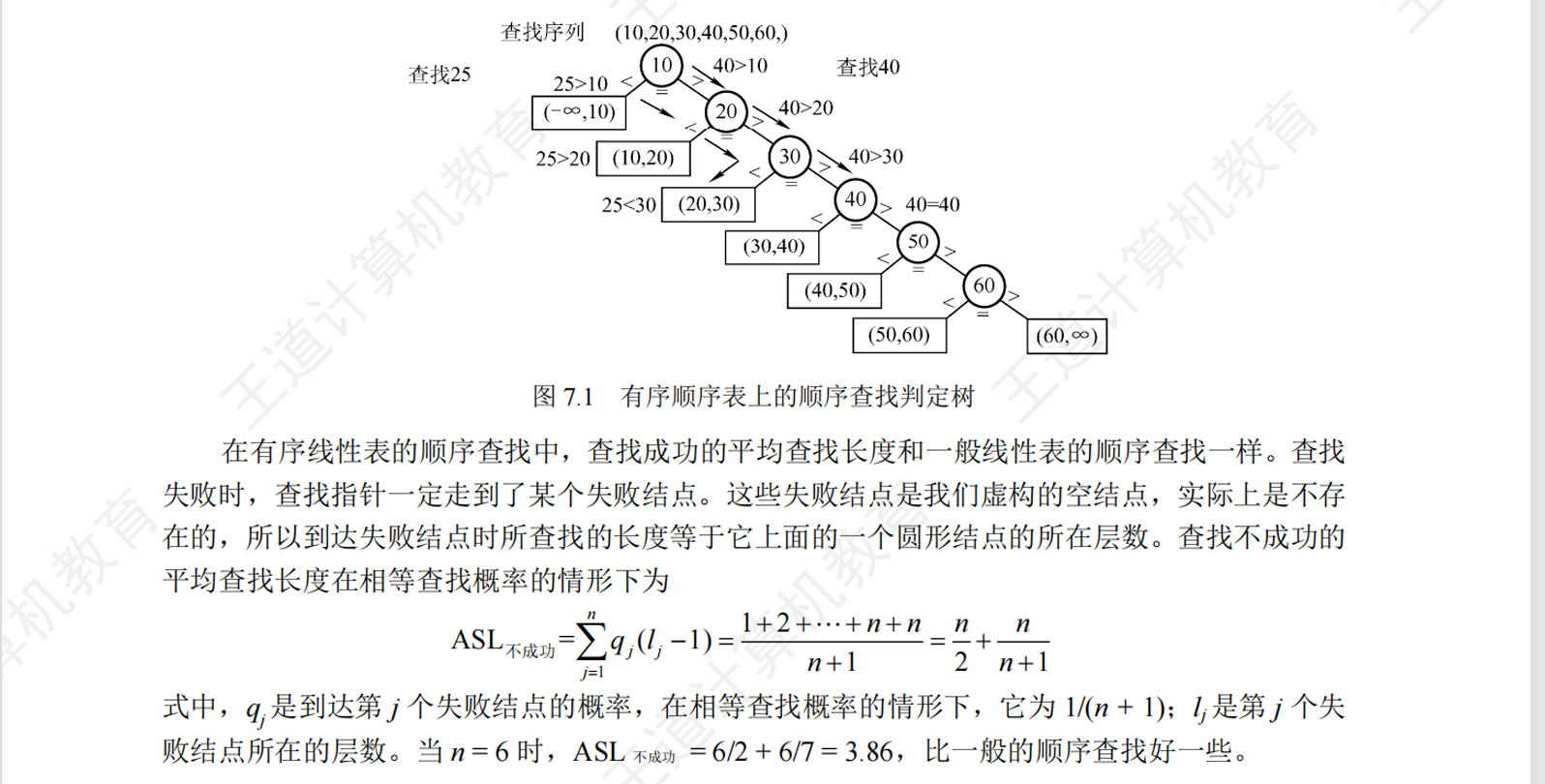
折半查找（二分查找）

int Binary_Search(SeqList L,ElemType key){
    int low = 0, high = L->length-1;mid = 0;
    while(low <= high){
        //注意这里为什么是等于，因为low与high始终在闭区间内运算，当low=high时，仍有一个值没有运算。
        mid = low +(high-low)/2;
        if(L.data[mid] > L.data[key]){
            high = mid -1;
        }else if(L.data[mid] < L.data[key]){
            low = mid +1;
        }else{
            return mid;
        }
    }
    return -1;
}

1. 需求有序排列
2. 仅适用于有序线性表（可以随机定位），不适合链式存储。
   
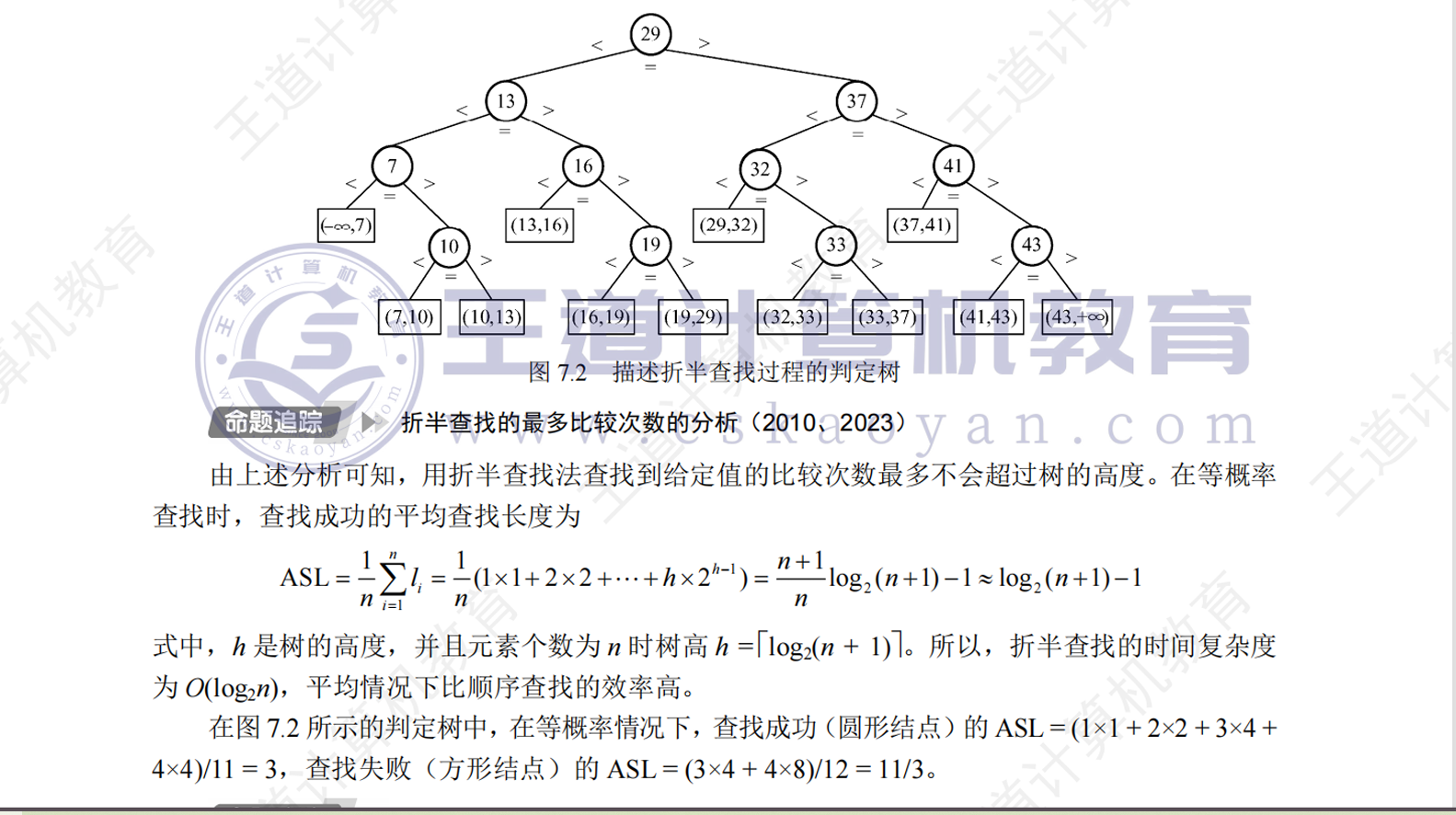
3. 时间复杂度为O(logn)，可以理解为每次排除一半的元素。

分块查找

1. 先将整个表分块（称为索引表），每个块中的元素不大于下一个块中的最小元素；再将索引表中的元素分为查找表。即这个过程有两个表。
2. ASL = ASL(索引表) + ASL(查找表)

• 若它们均采用顺序查找（总表长度为n,索引表被分为b块，查找表被分为s块）。ASL = (b+1)/2 + (s+1)/2，这里有n=sb。

树形查找

二叉排序树（BST）

说明与定义

1. 构造二叉排序树不是为了排序，而是为了加快插入与删除
2. 二叉排序树为递归定义：左子树结点值 < 根节点值 < 右子树结点值。因此中序遍历会得到递增的序列

查找

// 非递归
BSTNode *BST_Search(BiTree T , ElemType key){
    while(T != NULL && T->data != key){
        if(T->data < key){
            T = T->rchild;
        }else{
            T = T->lchild;
        }
    }
    return T;       //查找不到会返回NULL
}

//递归
BSTNode* BST_Search(BiTree T, ElemType key) {
    // 递归基（终止条件）：如果当前节点为空或节点的值等于key，返回当前节点
    if (T == NULL || T->data == key) {
        return T;
    }

    // 递归调用：根据key的大小决定向左子树还是右子树查找
    if (T->data < key) {
        return BST_Search(T->rchild, key);  // 查找右子树
    } else {
        return BST_Search(T->lchild, key);  // 查找左子树
    }
}

插入

int BST_Insert(BiTree T,ElemType k){
    if(T == NULL){
        T = (BiTree)malloc(sizeof(BiTree));
        T->data = k;
        T->lchild = NULL;
        T->rchild = NULL;
        return 1;
    }
    if(T->data == k){
        return 0 ;      //faild
    }
    if(T->data > k){
        //BST_Insert(T->lchild,k);          注意加上return，逐层返回
        return BST_Insert(T->lchild,k);
    }
    if(T->data < k){
        return BST_Insert(T->rchild,k);
    }
}

构造

void BST_Create(BiTree* T,ElemType str[],int n){
    int i = 0;
    while(i<n){
        BST_Init(T,str[i]);
        i++;
    }
}

删除

• 二叉排序树的删除

• 删除再插入结点，可能与原来的树不同

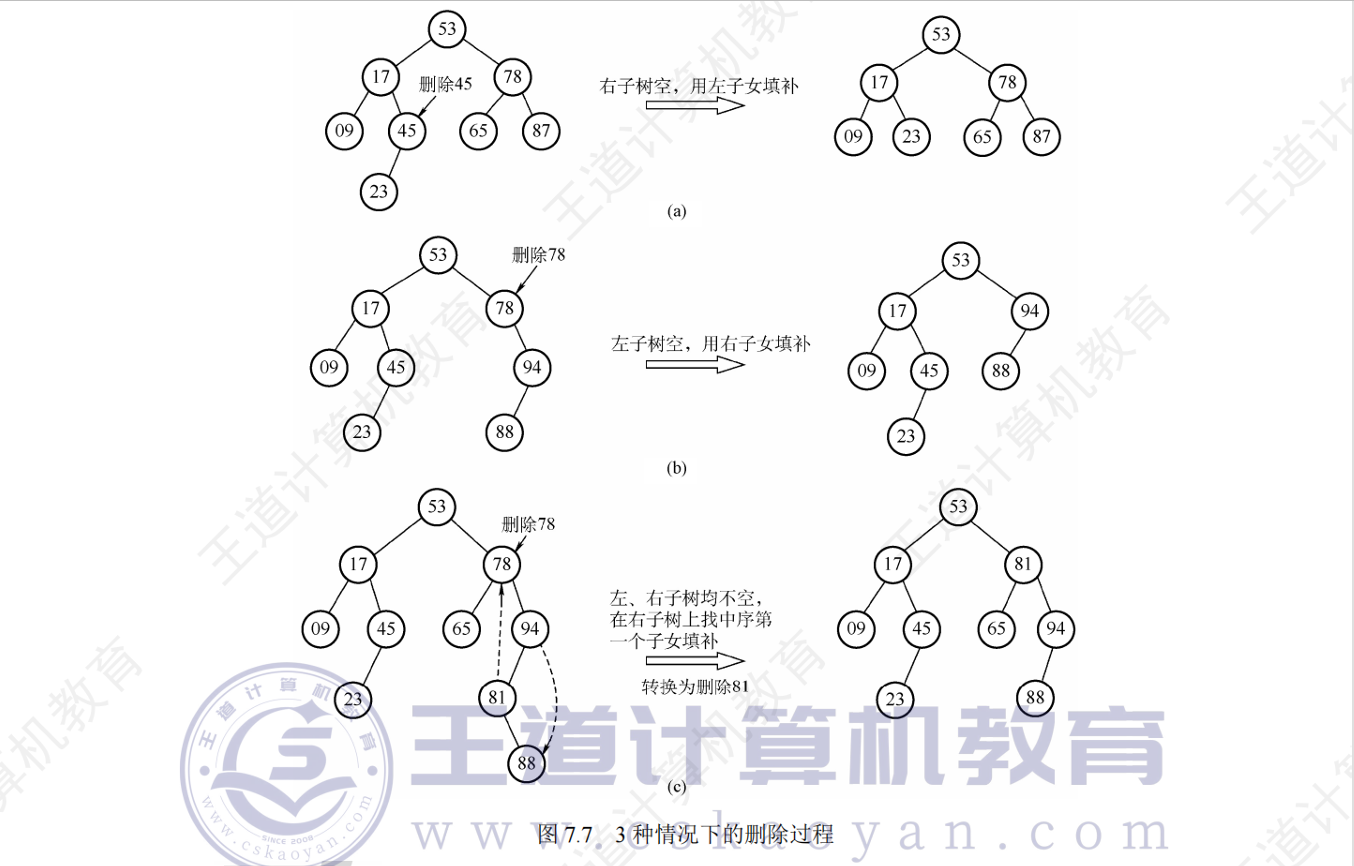
查找效率的分析

主要取决于树的高度。若左右子树的高度之差的绝对值不超过1（平衡二叉树），它的平均查找长度为O(logN)；若是只有一根分支的单支树，则为O(N)

比较二分查找与二叉排序树

平衡二叉树（AVL）

避免二叉树高度增长太快，降低二叉排序树的性能，引入了平衡二叉树。平衡二叉树要求左右子树的高度差（平衡）的绝对值不大于1，即只能是-1、0、1

平衡二叉树的插入

若插入一个结点导致了AVL的不平衡，则找到离插入结点最近的非法平衡因子结点，对以其为根的子树，旋转，手动调整其为平衡。（不计结论手动尝试也行）。

平衡二叉树的插入即构造过程。

平衡二叉树的删除

平衡二叉树的删除即：回溯到到被删除的结点的路径上的离该结点最近的不平衡的结点，如果调整后子树高度减一，可能需要对该结点的祖先调整平衡。

平衡二叉树的查找

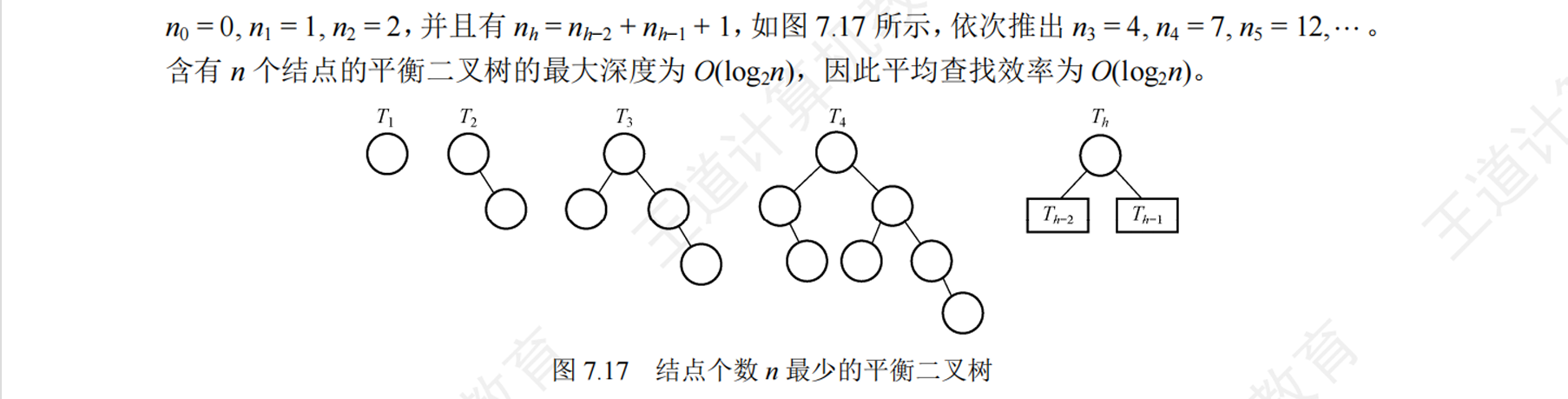
红黑树

在更新结点时，会频繁调整AVL的全局拓扑结构，花费代价大。适当的放款条件，便引入了红黑树。

性质：

• 只有红节点与黑结点
• 根节点为黑节点
• 叶节点、NULL、虚构结点都是黑色的
• 红节点不能相邻
• 任何一个节点到相同的任何一个叶节点的路径上经过的黑节点数量相同

B数和B+树

B树及其基本操作

m阶B树：平衡因子均为0的m路平衡查找树，或为NULL树，或满足以下性质

• 每个节点最多有m棵子树，即最多有m-1个关键字
• 若根节点不是叶节点，则至少有2棵子树，即1个关键字
• 除了根节点外的非叶子节点，至少有⌈m/2⌉棵子树，即至少⌈m/2⌉-1个关键字（当m==5，⌈5/2⌉==⌈2.5⌉==3）
• 非叶节点的结构如下：P0 K0 P1 K1 P2，P为指向子树根节点的指针，K为关键字（递增排序）
• 叶节点（这里指的是失败节点）出现在同一层次上

查找

查找到关键字–成功；查找到叶节点（指针为空）–查找失败

高度（不包括不带信息的那层）

设n为关键字，h为高度，m为阶数

1. n <= (m-1)*(1 + m + m^2 + ··· +m^(h-1)) = m^h -1
   即： h >= logm(n+1)

哈希表

1. 哈希函数

将查找表中的关键字映射成该关键字对应的地址，Hash(Key) = Address

2. 冲突

把两个或者两个以上的不同的关键字映射到同一地址。冲突难以避免，要设计好处理冲突的方法。

3. 哈希表

根据关键字直接访问的数据结构。理想情况下的哈希表查找时间复杂度与元素个数无关，为O(1)

4. 同义词

发生冲突的不同关键字